技業LOG
前回(と言っても一年近く経過していますね・・・。遅くなりました。)に引き続き、地図上に存在するエリアと現在地との関係性を計算機上で把握する手法の第2回目です。今回は、第3工程にあたる、「内外判定」について解説します。
現在地があるエリアの内側にいるか外側にいるかを考える場合、２次元平面上に存在する任意の点Pと多角形Tについて、点Pが多角形Tの内側にいるか外側にいるかを判定するにはどうしたらよいかを考えます。
この時、主に次の2つのアルゴリズムが利用されていることがわかりました。
- Crossing Number Algorithm
- Winding Number Algorithm
そこで、今回はこれらのアルゴリズムと実装方法(コード)について説明します。
1. アルゴリズムの概要
まずはそれぞれのアルゴリズムの概要を簡単に説明します。
1.1.Crossing Number Algorithm（交差数判定）の概要
このアルゴリズムは点Pから伸びる水平線Rが多角形Tの辺を交差する数(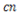
)で判定します。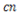が奇数ならば点Pは多角形Tの内側に、
逆に偶数または0ならば外側にいると判定します。
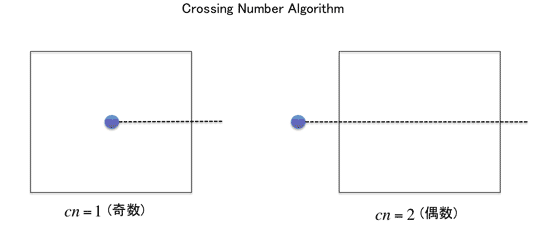
図 1-1: Crossing Number Algorithm概要図
このアルゴリズムは多角形Tが点Pの周りを回転した数(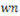
)で判定します。
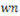が0である時に、すなわち多角形Tが点Pの周りを取り囲んでいない時、外側、それ以外の時は、内側にいると判定します。
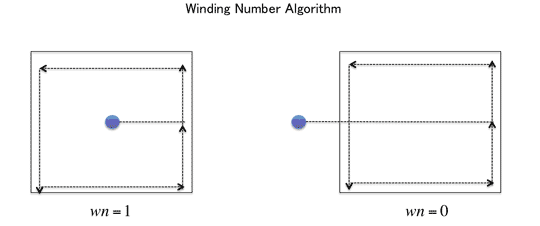
図 1-2: Winding Number Algorithm概要図
1.3.アルゴリズムの差異
ただし、これらの2つのアルゴリズムには判定結果が異なる状況が存在します。
それは多角形Tが自己交差を持ち、点Pが自己交差している領域に存在する場合です。図示すると、以下の様な状況です。
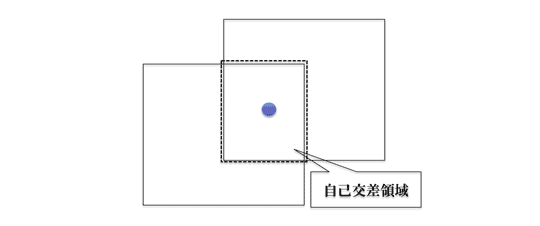
図 1-3: 自己交差領域
この時、
- Crossing Number Algorithmは外側
- Winding Number Algorithmは内側
であるとそれぞれ判定します。
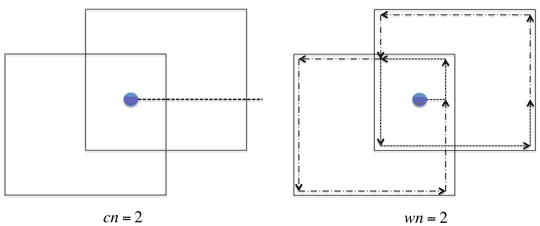
図 1-4: 自己交差領域での判定結果
自己交差を持つからと言って、多角形の領域が変わるわけではありませんので、回転数判定法の方がより直感的な結果であると言えます。
しかし、Crossing Number Algorithmの方が計算コストの小ささや実装が容易であることから、コンピュータグラフィックスの世界ではよく利用されているそうです。
なお、Winding Number Algorithmについてもアルゴリズムを工夫することで交差数判定法と同等の計算コストにすることができます。
この辺りの問題にも触れつつ、それぞれについて詳細と実装方法について説明していきたいと思います。
2. Crossing Number Algorithm
2.1.アルゴリズム
Crossing Number Algorithmでは、点Pから伸びる水平線Rが多角形Tを構成する辺
と交差する度に、内側にいるか・外側にいるかの判定が変わります(がインクリメントされる)。そして、水平線Rが多角形Tの外側に出た時の状態(の値)が判定結果となります。
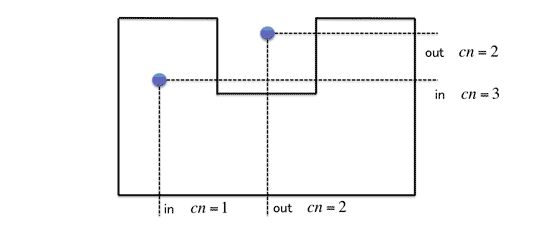
図 2-1: Crossing Number Algorithm
なお、Crossing Number Algorithmを実装するにあたり、1つ守らなくてはならないことがあります。それは、「必ず内側にいるか・外側にいるかの判定に関わる交差だけをカウントする」ということです。
つまり、水平線Rが多角形Tの頂点を通る、または辺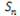
と水平である(重なる)といった特殊な状況を考慮しなければならないということです。
図 2-2: Crossing Number Algorithmの特殊ケース−1
他にも、点Pが多角形Tの辺の上に存在する場合を外側とするか内側にするかを考慮しなくてはいけません。この場合では、一般的に辺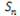が多角形Tの左側もしくは下側の辺である場合は内側、逆に右側もしくは上側の辺である場合は外側とします。こうすることで、万が一２つの多角形の辺が重なり、その上に点Pが存在する場合に点Pがどちらの多角形上に存在しているかを決定できます。
図 2-3: Crossing Number Algorithmの特殊ケース−2
これらの条件を考慮すると、次のルールを適用することで正しい判定が行えます。
- ルール1.上向きの辺は、開始点を含み終点を含まない。
- ルール2.下向きの辺は、開始点を含まず終点を含む。
- ルール3.水平線Rと辺が水平でない(がRと重ならない)。
- ルール4.水平線Rと辺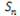の交点は厳密に点Pの右側になくてはならない。
図 2-4: 交差判定ルール
アルゴリズムの実装にあたっては、全ての辺に対してルール1からルール4を満たしているかを確認し、満たしている場合は水平線Rと辺は交差すると判定し、をインクリメントします。
2.2.コード
このアルゴリズムをコードで表す場合、多角形TはV[n]=V[0]とする頂点の配列V[n+1]となり、以下のようになります。
cn.js
var _polygon = function(){
this.v = new Array();
};
var polygon = new _polygon();
var v = function(x, y){
this.x = x;
this.y = y;
};
function init_polygon(){
polygon.v.push(new v(100,100));
polygon.v.push(new v(200,500));
polygon.v.push(new v(600,500));
polygon.v.push(new v(700,100));
polygon.v.push(new v(400,300));
polygon.v.push(new v(100,100));
}
var _point = function(x, y){
this.x = x;
this.y = y;
}
var point = new _point(300, 400);
function cn(){
cn = 0;
for(i = 0; i < poly.v.length - 1; i++){
// 上向きの辺。点Pがy軸方向について、始点と終点の間にある。ただし、終点は含まない。(ルール1)
if( ((polygon.v[i].y <= point.y) && (polygon.v[i+1].y > point.y))
// 下向きの辺。点Pがy軸方向について、始点と終点の間にある。ただし、始点は含まない。(ルール2)
|| ((polygon.v[i].y > point.y) && (polygon.v[i+1].y <= point.y)) ){
// ルール1,ルール2を確認することで、ルール3も確認できている。
// 辺は点pよりも右側にある。ただし、重ならない。(ルール4)
// 辺が点pと同じ高さになる位置を特定し、その時のxの値と点pのxの値を比較する。
vt = (point.y - polygon.v[i].y) / (polygon.v[i+1].y - polygon.v[i].y);
if(point.x < (polygon.v[i].x + (vt * (polygon.v[i+1].x - polygon.v[i].x)))){
++cn;
}
}
}
}
2.3.補足
なお、Crossing Number Algorithmの妥当性は「シンプルな閉曲線は２次元平面を２つの接続されたコンポーネント（境界のある内側と境界の無い外側）に分割する」という"Jordan Curve Theorem"(参考資料2)を基礎としています。
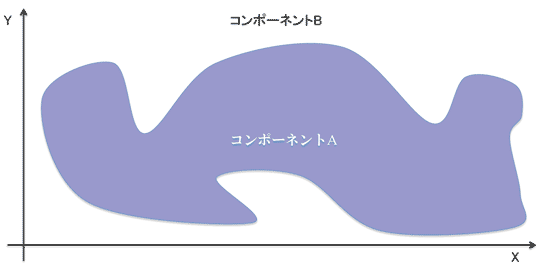
図 2-5: Jordan Curve Theorem
そのため、自己交差を持つ(シンプルでない)場合は、コンポーネントが3つ以上存在するため、前述したような結果になります。
3. Winding Number Algorithm
3.1.アルゴリズム
Winding Number Algorithmは、点Pを中心に多角形Tの辺を順番になぞっていった時に点Pの周りを何回回転するかを計算し、その数(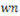)によって内側・外側の判定を行います。(参考資料4のIntuitive descriptionの項を参照)
この時、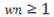
であれば多角形Tは点Pを取り囲んでいることになるので、点Pは多角形Tの内側にいると判定します。逆に、点Pが多角形Tの外側にいると判定されるのは
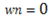の時だけです。
このような判定を行うため、Winding Number Algorithmは先述のCrossing Number Algorithmと異なり自己交差を持つ多角形についても点の内外判定を正確に行えます。
具体的な方法として、頂点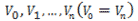
からなる多角形Tにおける、点Pと頂点
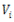からなる線分
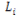、点Pと頂点
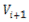からなる線分
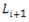がなす角度(符号付き、反時計回りを正、時計回りを負)の合計を考えます。
この時、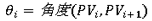
とすると、
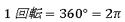なので、
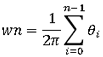
とできます。
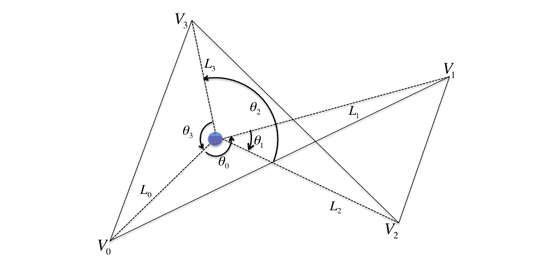
図 3-1: Winding Number Algorithm
さらに
であることから、
が成り立ちます。
この式を解くことによって内外判定を行うのですが、三角関数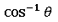
を利用しているため、前述したとおり交差数判定法よりも計算コストがかかることがわかります。
しかし、アルゴリズムを改良することでCrossing Number Algorithmと同等の計算コストに抑えることができます。
それは、Crossing Number Algorithmと同様に点Pから伸びる水平線Rと多角形Tの辺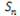が交差する数をカウントし、交差する辺が上向きであるか下向きで加算するか減算するかを変えるということです。
つまり、
- 上向きの辺と水平線Rが交差する場合は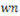を+1
- 下向きの辺と水平線Rが交差する場合はを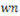-1
とします。
こうすることで、Crossing Number Algorithmに
- ルール5.上向きの辺と交差する場合、を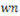+1する。
- ルール6.下向きの辺と交差する場合、を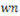-1する。
を追加したアルゴリズムとなり、三角関数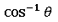を計算することなく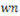を得ることができます。
この手法については少々内容が複雑なので、補足として後述させてもらいます。
3.2.コード
Crossing Number Algorithmと同等のアルゴリズムで考えた場合、こちらも多角形TをV[n]=V[0]とする頂点の配列V[n+1]として、以下のようになります。
wn.js
var _polygon = function(){
this.v = new Array();
};
var polygon = new _polygon();
var v = function(x, y){
this.x = x;
this.y = y;
};
function init_polygon(){
polygon.v.push(new v(100,100));
polygon.v.push(new v(200,500));
polygon.v.push(new v(600,500));
polygon.v.push(new v(700,100));
polygon.v.push(new v(400,300));
polygon.v.push(new v(100,100));
}
var _point = function(x, y){
this.x = x;
this.y = y;
}
var point = new _point(300, 400);
function wn(){
wn = 0;
for(i = 0; i < poly.v.length - 1; i++){
// 上向きの辺、下向きの辺によって処理が分かれる。
// 上向きの辺。点Pがy軸方向について、始点と終点の間にある。ただし、終点は含まない。(ルール1)
if ( (polygon.v[i].y <= point.y) && (polygon.v[i+1].y > point.y) ) {
// 辺は点pよりも右側にある。ただし、重ならない。(ルール4)
// 辺が点pと同じ高さになる位置を特定し、その時のxの値と点pのxの値を比較する。
vt = (point.y - polygon.v[i].y) / (polygon.v[i+1].y - polygon.v[i].y);
if(point.x < (polygon.v[i].x + (vt * (polygon.v[i+1].x - polygon.v[i].x)))){
++wn; //ここが重要。上向きの辺と交差した場合は+1
}
}
// 下向きの辺。点Pがy軸方向について、始点と終点の間にある。ただし、始点は含まない。(ルール2)
else if ( (polygon.v[i].y > point.y) && (polygon.v[i+1].y <= point.y) ) {
// 辺は点pよりも右側にある。ただし、重ならない。(ルール4)
// 辺が点pと同じ高さになる位置を特定し、その時のxの値と点pのxの値を比較する。
vt = (point.y - polygon.v[i].y) / (polygon.v[i+1].y - polygon.v[i].y);
if(point.x < (polygon.v[i].x + (vt * (polygon.v[i+1].x - polygon.v[i].x)))){
--wn; //ここが重要。下向きの辺と交差した場合は-1
}
}
// ルール1,ルール2を確認することで、ルール3も確認できている。
}
}
cn.jsと見比べてみると、ほとんど違いがないことがわかります。
3.3.補足
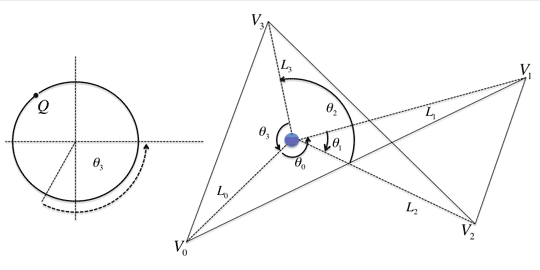
Winding Number Algorithmをより一般的に解説すると、二次元平面上の点Pの周囲の閉連続曲線についての回転数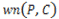
を考えます。
閉連続曲線をCとすると、
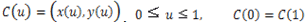
となります。また、点Pは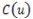
上に存在しないものとします。
この時、点Pから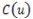へのベクトル
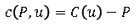
と、その単位ベクトル
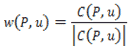
を定義すると、曲線C上の点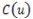を単位円
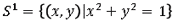上の点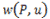
に写像している連続関数
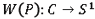
が成り立ちます。
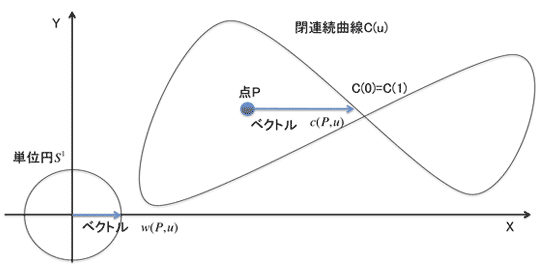
図 3-2: 点P と閉連続曲線C
この写像は
として、極座標上に表すことができます。
つまり、回転数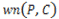は「閉連続曲線Cについて、uを0から1まで変化させた時に単位円
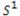を何周したか」に置き換えることができます。
これは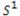のホモトピー類に相当し、以下の式が成り立ちます。
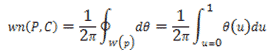
そして、さらにこれを多角形に置き換えると先程の
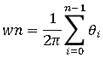
が成り立ちます。
次に、アルゴリズムの改良です。
先ほどの単位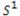上に任意の点Qをとったとします。
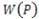は、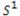を周回するので、点Qを何回か通過します。
仮に、
点Qを反時計回りに通過する場合に+1
点Qを時計回りに通過する場合を-1
とすると、その積算は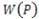が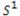を周回した回数
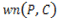とできます。
点Pが閉連続曲線Cの内側にある場合、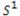上の点Qを少なくとも1回は通過するので、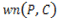は必ず0より大きくなります。
これを3.1.で示した多角形Tに置き換えて考えてみましょう。
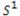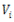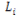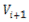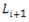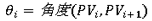つまり、点Pと多角形Tの単位円上に点Qを設置し、点Pと頂点からなる線分と点Pと頂点からなる線分がなすで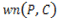を考えます。
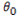の場合、
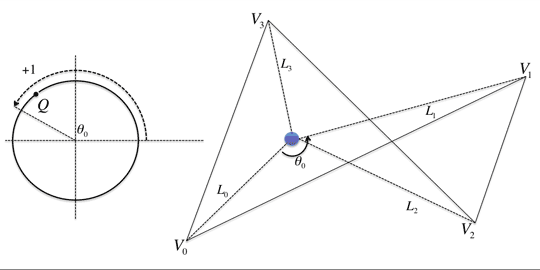
点Qを反時計回りに通過しているので、は+1されます。
の場合、
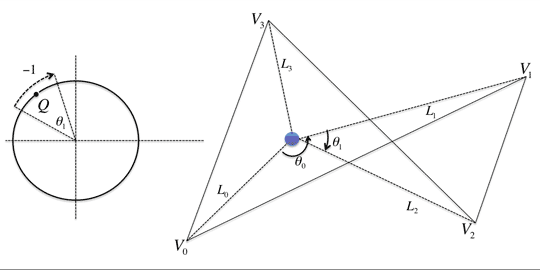
点Qを時計回りに通過しているので、は-1されます。
の場合、
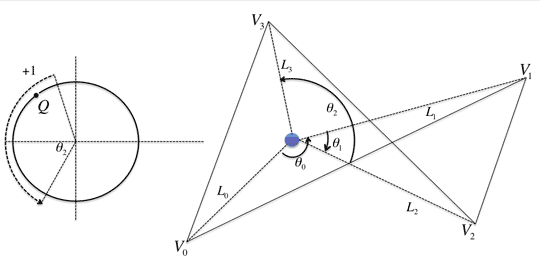
点Qを反時計回りに通過しているので、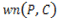は+1されます。
最後に
の場合、
今回は点Qを通過しないので、は変化しません。
そして、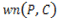 = 1となり、点P は多角形T の内側にいると判定できます。
点Qは単位円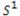上に存在するので、そのベクトルは、点Pと多角形Tがなすいずれかのベクトルの単位ベクトルです。
また、点Pから伸びる水平線Rは、点Pが多角形Tの内側にある場合には多角形Tのいずれかの辺と必ず交差します。この時、点Pとその交点Oがなす線分POは点Pと多角形Tのベクトルとなり、その単位ベクトルは単位円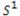上の点Qとなりえます。
つまり、Crossing Number Algorithm同様、点Pから伸びる水平線Rと多角形Tとの交点について考えることでを求めることができます。
そして、交点で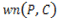を+1するか-1については辺の向きで決定できます。
つまり、
上向きの辺である場合、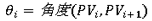は正なので、点Qを反時計回りに通過するので 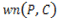を+1
下向きの辺である場合、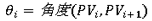は負なので、点Qを時計回りに通過するので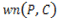を−1
とできます。
上記の事柄をCrossing Number Algorithm同様ルール化すると、
- ルール1.上向きの辺は、開始点を含み終点を含まない。
- ルール2.下向きの辺は、開始点を含まず終点を含む。
- ルール3.水平線Rと辺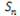が水平でない(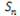がRと重ならない)。
- ルール4.水平線Rと辺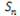の交点は厳密に点Pの右側になくてはならない。
- ルール5.上向きの辺と交差する場合、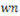を+1する。
- ルール6.下向きの辺と交差する場合、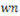を-1する。
となります。
- ルール1からルール4は点Pが辺と交差するかの判定
- ルール5とルール6の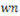を+1するか-1するかの判定
です。
簡単に図示すると以下のようになります。
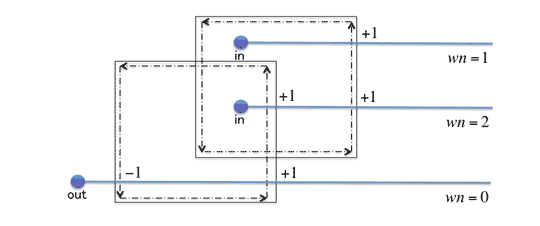
図 3-3: 簡略化したWinding Number Algorithm
Crossing Number Algorithmと同じに見えますが、通常のWinding Number Algorithmeと同様に自己交差領域でも内側であると判定できていることがわかります。
4.まとめ
今回は、現在地とエリアを２次元平面上に存在する任意の点Pと多角形Tに置き換え、点Pの多角形Tに対する内外判定を行うアルゴリズムについて解説しました。なかなか複雑な内容だったと思いますが、おわかりになりましたでしょうか。もっと理解を深めたいという方は、後述している参考資料を読み解いてみてください。
技業LOG