技業LOG
このテーマでは、地理情報システムの開発過程で得られた、地図上に存在するエリアと現在位置との関係性を計算機上で把握する手法について全3回で解説します。
弊社は2010年度より財団法人 衛星測位利用推進センター主催の準天頂衛星民間実証実験に参加しています。実証実験では位置情報を利用したコンテンツ配信サービスや防災サービスの構築を目指し、地理情報システム(GIS)の開発およびフィールドテストに取り組んでいます。
この地理情報システムの開発過程で、地図上に存在するエリアと現在位置との関係性(近接しているか、内側にいるか、外側にいるか)は、以下の工程を経ることで計算機上でも把握できることがわかりました。
- 近接候補エリアの抽出
- 近接候補エリアと現在位置との距離の計算
- 内外判定
今回は、第2工程である「近接候補エリアと現在位置との距離の計算」について解説します。エリアと現在位置をXY平面上の多角形と点とに置き換えて距離を定義し、プログラム可能な計算式を導き出します。
多角形と点の距離
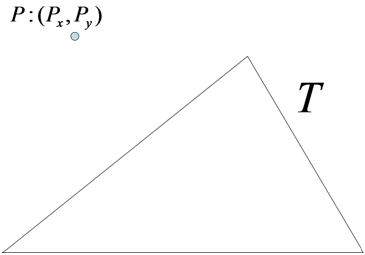
多角形と点の距離は、多角形を構成する各線分と点との距離の計算によって求めることができます。今回は三角形Tと任意の点Pを例に解説を進めます。
図1: 三角形Tと任意の点P
三角形Tと点Pの距離dは、Tの各線分(L1,L2,L3)とPとの距離(d1,d2,d3)のうち、その値が最小(d_min)となるものです。
図2: 三角形Tと点Pとの距離
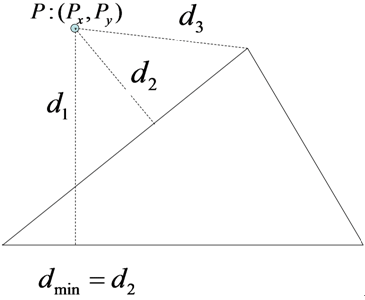
これは、三角形のみならず全ての多角形においても同様です。つまり、多角形と点の距離は多角形を構成する線分と点との距離の計算によって求まることができます。
次章では、線分と点との距離の定義について解説します。
線分と点の距離
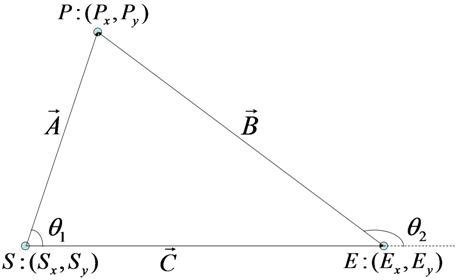
始点Sと終点Eとを結ぶ線分Lと任意の点Pを例にとり、線分と点との距離について解説します。
図3: 線分Lと任意の点P

始点Sから点PへのベクトルをA、終点Eから点PへのベクトルをB、始点Sから終点EへのベクトルをC。また、AとCがなす角をθ1、BとCがなす角をθ2と定義します。
図4: 線分Lと点Pの関係
この時、θ1とθ2の値(すなわち線分Lと点Pとの位置関係)によって、距離の定義は3つに分類されます。
- θ1<90°かつθ2>90°(条件1)
- θ1≧90°かつθ2>90°(条件2)
- θ1<90°かつθ2≦90°(条件3)
それぞれの条件での距離は以下の通りです。
条件1の場合、
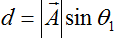
図5:条件1での距離d
条件2の場合、
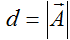
図6:条件2での距離d
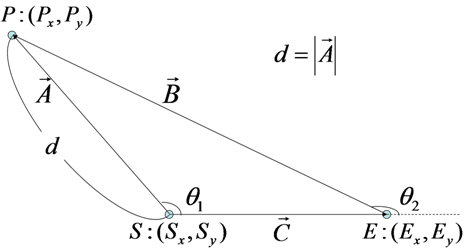
条件3の場合、
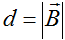
図7:条件3での距離d
次章では、これらの定義からプログラム可能な計算式を導き出します。
プログラム可能な計算式
条件1から条件3、それぞれの定義からプログラム可能な計算式を解説します。
条件1の計算式
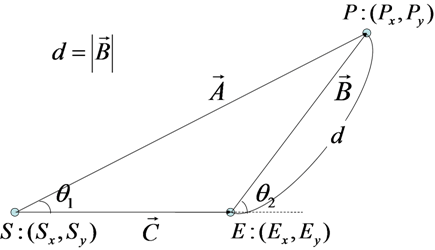
条件1の計算式を求めるために、まずCとAとの外積CxAを考えます。
図8:CとAとの外積CxA
ベクトルの外積の絶対値は、それぞれのベクトルを線分とした場合の平行四辺形の面積と等しくなります。すなわち、
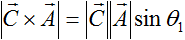
が成り立ちます。
図8:CとAとの外積と平行四辺形

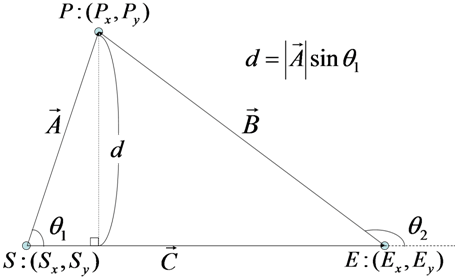
また、条件1の時に距離は
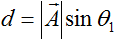
であることから、
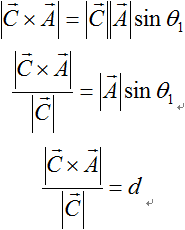
となります。
上記の式を展開すると、線分Lと点Pとの距離は、
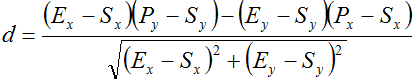
となり、これがプログラム可能な計算式となります。
- ※
条件2の計算式
条件2の時、始点Sと点Pとの距離が線分Lと点Pとの距離となります(図6)。したがって、
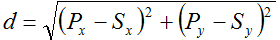
となり、これがプログラム可能な計算式となります。
条件3の計算式
条件3の時、終点Eと点Pとの距離が線分Lと点Pとの距離となる(図7)。したがって、
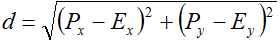
となり、これがプログラム可能な計算式となります。
以上が線分Lと任意の点Pの距離を求めるプログラム可能な計算式です。次章では、線分Lと点Pがどの条件と一致するか (すなわちどのような位置関係にあるか)を判定する方法について解説します。
線分と点の位置関係の判定
線分Lと点Pの位置関係はベクトルの内積によって判定可能です。
第3章より、線分Lと点Pの位置関係は以下の3つに分類されます。
- θ1<90°かつθ2>90°(条件1)
- θ1≧90°かつθ2>90°(条件2)
- θ1<90°かつθ2≦90°(条件3)
また、cosθは以下の性質を持ちます。
- 0°≦θ≦90°の時、1≧cosθ≧0
- 0°<θ≦180°の時、0>cosθ≧-1
よって、
- θ1<90°かつθ2>90°(条件1)
- θ1≧90°かつθ2>90°(条件2)
- θ1<90°かつθ2≦90°(条件3)
は、
- cosθ1>0かつcosθ2<0(条件1)
- cosθ1≦0かつcosθ2<0(条件2)
- cosθ1>0かつcosθ2≧0(条件3)
と置き換えられます。
さらに、余弦定理より線分Lと点Pでは
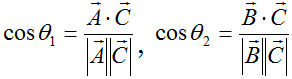
が成り立ちます(図4)。
|A|,|B|,|C|は絶対値であるためcosθ1,cosθ2の分母は必ず正となります。加えて、ベクトルが直交する時(θ=90°)の内積は0となるので、cosθ1,cosθ2の正負および0か否かはベクトルの内積で求まります。
このことから、
- cosθ1>0かつcosθ2<0(条件1)
- cosθ1≦0かつcosθ2<0(条件2)
- cosθ1>0かつcosθ2≧0(条件3)
は、
- A・C>0かつB・C<0(条件1)
- A・C≦0かつB・C<0(条件2)
- A・C>0かつB・C≧0(条件3)
となります。
よって、線分Lと点Pの位置関係がどの条件に該当するかはベクトルの内積で判定可能であることがわかります。
なお、ベクトルの内積はそれぞれ以下の式で計算可能です。
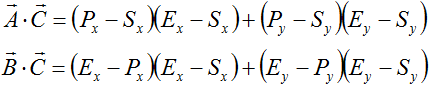
まとめ
今回は、近接候補エリアと現在位置をXY平面上の多角形と点とに置き換えた場合、どのように距離を計算するかについて解説しました。解説を通して、多角形と点の距離はベクトルの内積、外積を用いることで計算可能であることをご理解されたと思います。
次回は、第3工程である内外判定、つまり現在位置があるエリアの内側か外側かを判定する手法について解説します。
技業LOG